Les contours actifs
Snake classique
Le snake classique défini par Kass, Witkin et Terzopoulos en 1987, est une courbe paramétrée C(q) =(x(q); y(q)) qui sera attirée par les zones de forts gradients , c’est à dire où la norme du gradient 
d’un point I sera élevée.
Les paramètres de cette courbe peuvent être l’élasticité, la tolérance au bruit, etc.
Cette manœuvre demande une certaine énergie constituée d’une énergie interne et d’une énergie externe :
Une énergie supplémentaire peut aussi être introduite : l’énergie de contexte ou de contrainte Econtexte ou encore l’énergie potentielle imposée par l’image pour plaquer la courbe sur les contours.
Un contour actif fermé est représenté par une matrice circulante pentadiagonale.
Algorithme de Greedy
Le déplacement et l’évolution du modèle de contour actif se fait par l’itération de l’algorithme « greedy » afin de minimiser l’énergie totale.
Pour chaque point vi du contour actif, cette fonctionnelle d’énergie E(ni) est calculée pour tous les points ni appartenant au voisinage de vi.
Le point ni0 caractérisé par l’énergie minimale E(ni0) est alors choisi pour remplacer vi si E(ni0) < E(vi).
Dans le cas contraire, le point de contour vi n’est pas modifié.
Ce mécanisme est répété jusqu’à convergence (lorsque le contour obtenu à l’itération t est identique à celui obtenu à l’itération t+1).
La déformation du contour dépend donc directement de la fonctionnelle d’énergie.
Pour minimiser l’énergie, l’algorithme doit satisfaire l’équation différentielle d’Euler-Lagrange définie ainsi :
La fonction réalisant un extremum de 
, sous hypothèses de régularité sur F, vérifie l'équation :
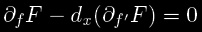
La fonction 
désigne la direction du gradient de J en f.
L’hypothèse de régularité nécessaire sur F est que la direction du gradient soit continue ce qui sera le cas dans la pratique.
Energie interne
L’énergie interne correspond à la morphologie et aux caractéristiques de la courbe telles que la courbure, la longueur, etc.
Elle va contrôler la régularité de la courbe aux premier et second ordres :
L’énergie interne est calculée à partir de trois forces appelées respectivement continuité, ballon, et courbure :
Eint = a . Econ + b . Ebal + c . Ecou
- La force de continuité Econ permet aux points de contour actif de se positionner à équidistance en influant sur le rayon de courbure la courbe du contour actif. Le snake tend alors à avoir la forme d’un cercle. Ainsi, l’énergie de continuité sert à calculer pour tous les temps la différence entre deux points successifs sur le contour actif et à maintenir cette équidistance sur tous les points.
- La force de ballon (introduite par Cohen) permet de modifier l’épaisseur du contour selon le signe du coefficient b associé à la force.
La force Ebal est définie par le produit scalaire entre le vecteur normal vi et le vecteur
. - La force de courbure a pour rôle d’éviter que le contour actif ne contiennent des points isolés et donc incohérents pour la forme régulière globale. L’énergie Ecou(ni) est donc proportionnelle à une expression discrète de la dérivée du second ordre.
Energie externe
L’énergie externe concerne l’image et ses propriétés/caractéristiques telles que la présence de bords ou encore de bruit.
Elle permet de s’assurer que le snake se trouve sur les bords l’image en maximisant la quantité de la norme gradient tout au long de la courbe et en minimisant donc son opposé :
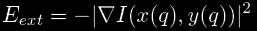
L’énergie est obtenue à partir de deux forces liées au gradient couleur et intensité de la composante couleur sur laquelle nous souhaitons nous rapprocher sur une image :
Eext = d . Egra + e . Ecoul
- La première force est basée sur une combinaison des gradients calculés sur les trois composantes couleur (rouge, vert, et bleu), fixant ainsi le contour sur les contours réels de l’image. L’estimation du gradient est calculée à l’aide de l’opérateur de Sobel puis seuillée, ce qui permet d’éliminer la plupart des contours non significatifs. Afin de réduire le temps de calcul, le gradient n’est calculé qu’une seule fois par image et sur une zone restreinte autour de la position initiale du contour.
- La deuxième force plus contextuelle utilise l’intensité d’une composante de l’image. Elle permet ainsi de conserver le contour externe des joueurs. L’énergie Ecoul est définie comme la différence entre l’intensité de la composante couleur et un seuil fixé TV.
Initialisation / Disposition
1. Initialisation sous forme de rectangle
Tout d’abord, il faut créer un rectangle dont les côtés sont parallèles aux contours de l’objet ou de la zone d’image d’intérêt.
La position et la taille du rectangle sont déterminées manuellement ou automatiquement de manière à ce qu’il englobe la totalité de la zone d’image et donc du supposé emplacement final du contour actif.
Puis, la position initiale du contour actif est obtenue en plaçant uniformément ses points sur le rectangle crée.
Déformation du contour actif
Le contour actif, dont le nombre de pointsdépend de la précision voulue, est donc prêt à être déformé et à se fixer progressivement autour de l’objet.
Le contour actif se voit réduire et ce jusqu’à convergence avec les forces composant l’énergie du snake.
Limites de la méthode
Bien que les calculs numériques soient rapides, certains problèmes liés à la méthode du snake peuvent apparaître selon le contexte dans lequel elle est utilisée.
En effet, si deux objets sont trop proches, il devient impossible pour le snake de détecter les contours d’un seul objet, d’autant plus s’ils sont en mouvement.
De plus, si un objet se trouve sur une zone de l’image très hétérogène, il sera difficile pour le contour actif de détecter les contours de ce premier.
Le choix de la paramétrisation du contour actif prend alors toute son importance dans le cas de la méthode du snake de Kass-Witkin-Terzopoulos, ce premier évoluant au cours du temps.
Ce qui engendre, de plus, un autre problème qui est celui de la topologie étant donné que le contour actif ne change pas de forme au cours du temps, car étant incapable de détecter plusieurs objets dans une image.
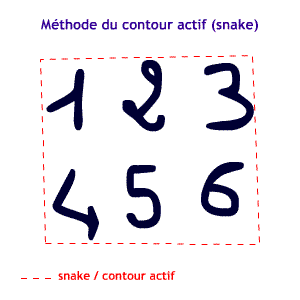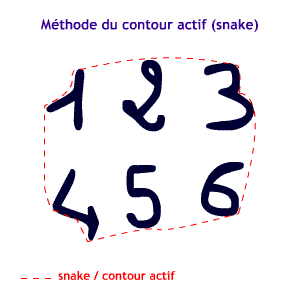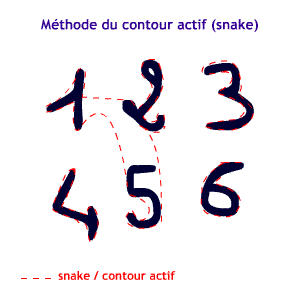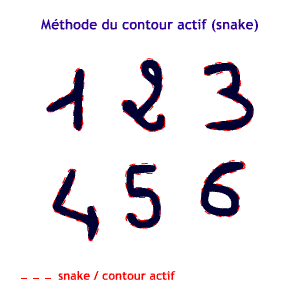
Approche géodésique
Afin de palier aux problèmes rencontrés avec la méthode du snake de Kass, Witkin et Terzopoulos, il existe une autre méthode de contour actif, le snake de Caselles-Kimmel-Sapiro et Kichenassamy établit en 1995.
Résolution du problème de la paramétrisation
Il s’agit de redéfinir la longueur de la courbe paramétrique par la formule suivante :
L’énergie pour un élément de longueur dq d’un élément dépendra alors de la valeur du gradient en ce point.
Ainsi, un déplacement suivant une ligne dont le bord est à fort gradient nécessitera moins d’énergie que si le snake se trouve en présence d’une zone à faible gradient.
La solution recherchée sera alors celle pour laquelle le snake sera minimisant en « coût » d’énergie, soit une géodésique de cette nouvelle longueur.
Résolution du problème du changement de topologie
Le snake est représenté par une fonction de type u(x,y) dans le même domaine que l’image donnée par la fonction I(x,y)et dont le snake sera la courbe de niveau zéro(voir méthode des courbes de niveaux).
On calcule l’équation d’évolution de la fonction u dans le temps qui permettra de gérer au fur et à mesure, automatiquement et naturellement, les changements de topologie rencontrés par le snake lors de son évolution.
Cette équation d’évolution est obtenue à partir de l’équation d’Euler-Lagrange :
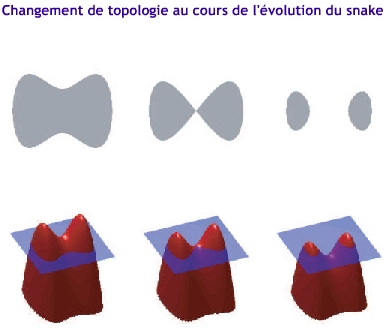
Inconvénients
Les calculs numériques restent plus lents que le snake précédent. De plus, la solution finale dépend de la condition initiale ce qui peut engendrer des problèmes de minima locaux dans la fonctionnelle énergétique. Enfin, le contour actif ne détecte que les bords des objets dans les images alors que nous souhaiterions aussi trouver les régions homogènes.
Méthode des ballons
Le modèle des ballons permet l’extraction d’un objet à contour fermé à partir d’un contour actif positionné à l’intérieur de l’objet. Le snake gonfle alors à l’intérieur de l’objet, tel un ballon, et ce jusqu’à ce qu’il soit freiné par les forces dues au gradient du contour de l’objet en question, compensant les forces de ballonnement. Le gonflement du contour actif s’arrête donc dès qu’il se trouve sur le contour de l’objet.
Défauts du modèle
Cependant ce modèle connaît quelques défauts. Le principal défaut étant que la courbe du contour actif doit être assez proche des points du contour de l’objet pour être attirée. Dans le cas contraire, le contour actif risque de s’effondrer sur lui-même et converger vers un point. De plus, des maxima du gradient dus au bruit possible autour du contour actif peuvent stopper son évolution.
Solution possible
Une solution proposée par Laurent D. Cohen au problème de l’effondrement en un point consiste à ajouter une force supplémentaire au contour actif afin de lui donner un comportement plus dynamique : la force du ballon. En effet, la modélisation mécanique du contour actif l’amène à se conduire tel un ensemble de masses reliées par des ressorts de longueur nulle. Ainsi, il suffit de rajouter une normale au contour actif orientée vers l’extérieur afin que celui-ci gonfle comme un ballon. Il n’aura alors plus tendance à s’écraser sur lui-même, passer au-delà des pics de gradient dus aux bruit tout en étant beaucoup moins sensible lors de son initialisation.
Prior Shape
On utilise un snake similaire au snake adoptant l’approche géodésique et la représentation par level-set auquel on ajoute un terme dans l’énergie.
Ce snake dont l’auteur est Y. Chenen a pour but de localiser dans une image, une figure dont on connaît la forme générale tout en supprimant toutes les informations relatives à son emplacement, son orientation et son échelle.
Ce snake permet de reconstituer des objets sur une image fragmentaire en recherchant le contour le plus adapté à chaque fois que la prior shape (« la forme a priori »), notée C*, diffère.
On souhaite alors trouver la courbe C, l’échelle m, la matrice de rotation R d’angle Ø et le vecteur de translation tels que mRC+T et C* soient proches.
Il s’agira, à l’aide de l’équation d’Euler-Lagrange, de minimiser l’énergie traduite par :
δ : masse de Dirac en zéro.
d : fonction de distance C*.
λ : paramètre permettant de régler l’importance relative des deux termes :
et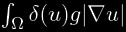 
Stochastique
Le snake stochastique permet d’éviter les problèmes de minima locaux. Pour cela, il faut perturber le snake censé avoir atteint le minimal local en le poussant à aller plus profondément et ainsi avoir plus de chance d’atteindre le minimal local. Cette perturbation se fait par l’ajout d’un terme brownien à l’énergie ; il s’agit de l’algorithme du recuit simulé.
Champs d'application
On retrouve ce modèle en imagerie médicale, en cartographie, dans la reconnaissance de forme, la simulation, le suivi de scène ou encore la segmentation d’image.
Des logiciels de traitement d’images utilisent les contours actifs tels que Photoshop ou Gimp avec par exemple l’utilisation de l’outil « baguette magique » dont le but est de détecter les contours d’objets d’une image dont le paramètre est le taux de tolérance du bruit ou de la couleur.