Approche mathematique
On considère pour l'instant un signal continu f monodimensionnel.
Bases de la détection
Rappels sur le filtrage
Le filtrage spatial d’une image I consiste à convoluer cette image considérée comme une fonction I(x,y) avec une fonction f(x,y) appelée réponse impulsionnelle du filtre.
Ces filtres peuvent être linéaires ou non-linéaires.
Un filtre linéaire est un filtre qui applique un opérateur linéaire au signal d’entrée. Cela signifie que le résultat du filtrage se présente comme une combinaison linéaire des niveaux de gris d’un voisinage de l’image. Les filtres passe-haut font ressortir les contours, les filtres passe-bas floutent l’image.
La convolution est souvent utilisée pour le lissage, l’accentuation et la détection des contours.
L’accentuation et la détection sont en quelque sorte les opérations contraires du lissage : On amplifie les hautes fréquences spatiales, caractéristiques des transitions rapides.
La plupart du temps il faut combiner filtre non linéaire et filtre linéaire afin de détecter ce que l'on souhaite tout en faisant abstraction du bruit.
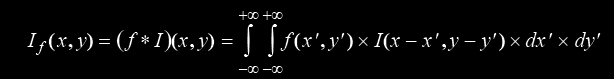
Formule du filtrage - cas discret (cas des images numériques) :
Présentation des approches classiques
Opérations sur la dérivée
On utilise les dérivées car elles éliminent les variations lentes et détectent les variations locales d'intensité des pixels.
Méthode 1. Calcul de f’(x)
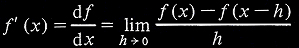
Si l'on prend l'unité comme période d’échantillonnage, les valeurs de x les plus proches le sont pour h=1. On obtient donc une dérivée approchée du signal en calculant f(x) – f(x-1), ce qui correspond à une convolution par la matrice [-1 1 0].
Avec un signal d'origine monodimensionnel de 7 échantillons unité provenant d'un rectangle :
On obtient, suite à cette convolution :
Les bords sont détectés. On observe que cela revient à faire la différence entre le signal et le signal décalé d’une unité vers la droite.
Inconvénient : La transition ascendante est bonne mais la transition descendante est décalée d’une unité vers la droite.
Méthode 2. Calcul à partir de la Méthode de Taylor
Cette méthode remédie au décalage précédemment observé.
On a :
Soit : 
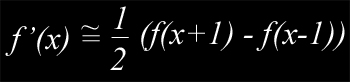
A un facteur ½ près, on peut réaliser cette opération par convolution avec la matrice M=[-1 0 -1]. On obtient :
Inconvénient : Cette fois-ci, la symétrie est bonne mais la largeur des bords détectés est double.
On se place maintenant dans le cas d'un signal bidimensionnel.
La matrice 3x3 réalisant la dérivation partielle horizontale (δ ∂f /δ ∂x) est :
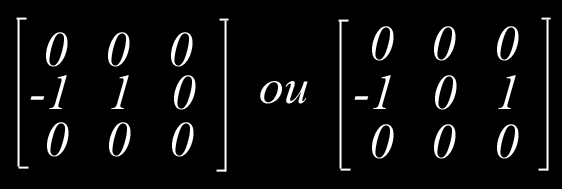
La matrice 3x3 réalisant la dérivation partielle verticale (δ ∂f /δ y) est :
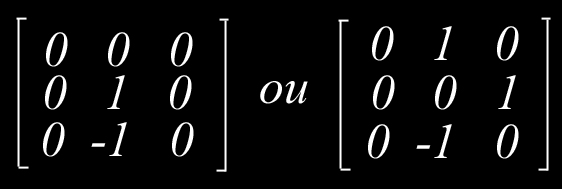
Méthode 3. Dérivée partielle seconde
On pousse la dérivée partielle de Taylor jusqu’à au second ordre pour trouver une expression approchée de (∂(δ ² f ) /δ ∂x ²) :
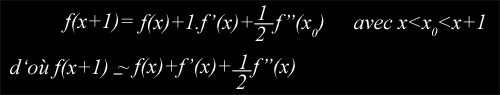
En remplaçant f’ par f(x)-f(x-1) :
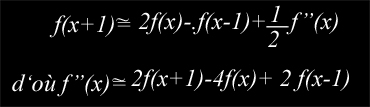
Au facteur 2 près on obtient la matrice :
Et, pour (∂(δ ² f ) /δ ∂y ²) :
Remarque générale sur les opérateurs de dérivation : Ils font apparaître des valeurs négatives. On ajoute une constante positive en guise de correctif.
Deux grands types de méthodes dérivatives
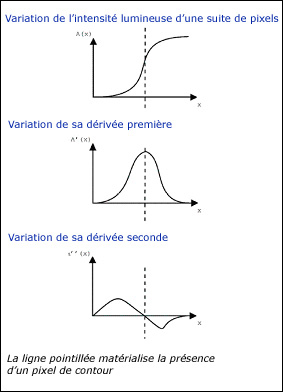
On distingue donc deux types de méthodes dérivatives : celles basées sur la dérivée première et l’extraction de ses maxima locaux, et celle basée sur la dérivée seconde et l’extraction de ses passages par zéros. Les premières s’appuient sur des filtres étroits basés sur le gradient, les secondes sur des filtres larges basés sur le laplacien.
Introduction au Gradient
Définition
Le gradient, en un pixel d'une image numérique, est un vecteur caractérisé par son amplitude et sa direction :
- L'amplitude est liée à la quantité de variation locale des niveaux de gris.
- La direction est orthogonale à la frontière qui passe au point considéré.
Calcul
Il faut choisir deux directions privilégiées (naturellement celles associées au maillage : ligne et colonne) orthogonales, sur lesquelles on projette le gradient. Puis on effectue deux calculs identiques donnant le vecteur gradient en chaque point (x,y) de l'image :
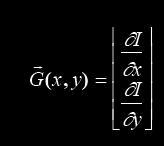
Propriétés
- Le gradient est orthogonal et normal aux courbes de niveaux de l’image.
- La direction du gradient est orthogonale à la frontière qui passe au point considéré et maximise la dérivée directionnelle.
- Sa norme est la valeur de cette dérivée.
- Le gradient est orienté dans le sens de croissance du champ, cette croissance étant d’autant plus forte que la normale du gradient est importante (d’après l’inégalité de Cauchy-Schwarz).
Introduction au Laplacien
Définition
Le laplacien est un opérateur différentiel égal à la somme de toutes les deuxièmes dérivées partielles non mixtes d'une variable dépendante.
Calcul
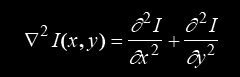
Propriété
L'opérateur laplacien est linéaire.
Dérivation par différence finie
Filtres de dérivée première
Longueur du vecteur gradient
Calcul
A partir des propriétés du gradient, on peut considérer que le contour d’une image correspond au gradient dont la norme est à son maximum. Le module du gradient est défini par :
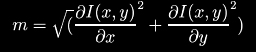
Masque associé
En appliquant la formule du gradient à une image (fonction de deux variables) on obtient deux dérivées partielles, suivant x (colonnes) et suivant y (lignes) dont les masques sont :
Avantages et inconvénients
Le problème est que la dérivation accentue le bruit (pixels parasites de répartition aléatoire). Des filtres dérivés plus robustes, ont donc été proposés parmi lesquels Roberts, Prewitt, Sobel, Kirsch, Robinson.
Roberts
Calcul
Il s’effectue sur quatre points.Masques associés
Avantages et inconvénients
L’avantage de cet opérateur est sa rapidité; le calcul de l’amplitude consistant à faire la somme des valeurs absolues de la différence de deux pixels. De plus, il conserve les détails car il utilise des matrices 2x2 et donc agit localement.
L’inconvénient de cet opérateur est son extrême sensibilité au bruit du fait de sa petite taille.
Prewitt
Il est directionnel.
Calcul
Il s’effectue sur 9 points : On réalise la moyenne locale sur 3 points en même temps que la dérivation.
C'est une convolution entre un opérateur de lissage et un opérateur de dérivation.
Masque associé
Inconvénient
Cet opérateur est sensible aux bruit.Sobel
Ce filtre est directionnel.Calcul
Le calcul s’effectue sur 9 points. Il s’agit d’une variante du filtre de Prewitt qui privilégie le calcul suivant certaines directions (horizontale, verticale, obliques).
On dénombre huit directions possibles : N-S ; S-N ; O-E ; E-O ; NE-SO ; SO-NE ; NO-SE ; SE-NO.
Ex : la dérivée NE-SO accentue les contours orientés NO-SE et engendre un effet d’optique d’ombre portée sur l’image, comme si elle était éclaire par une lumière rasante provenant du NO.
Masques associés
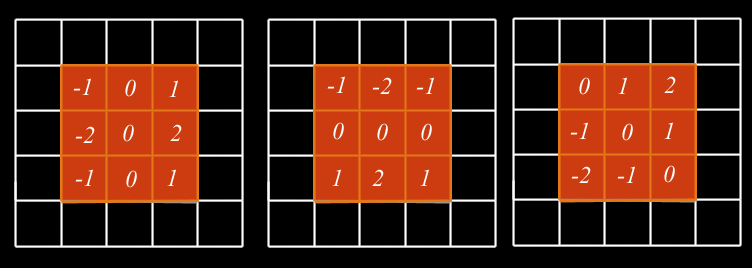
Avantages et inconvénients
Le détecteur de Sobel donnera de meilleurs résultats au prix d'une complexité de calcul plus grande que celle de Roberts.
Kirch
Il s’agit d’une variante classique du filtrage gradient.Calcul
La méthode proposée consiste à filtrer l’image avec 8 masques directionnels.
L’orientation du contour (orientation du filtre + 45°) est dans ce cas déduite par le filtre donnant le résultat le plus élevé ( qui est considéré comme représentant l’intensité du gradient).
Masque associé
On utilise un facteur de normalisation 1/15.
Inconvénient
Le coût d'implémentation des masques directionnels est élevé.
Conclusion sur ces variantes du gradient
L'ensemble des opérateurs précédents, issus du gradient, sont moins précis que le filtre gradient pur mais plus fiables car plus robustes.
Filtres de dérivée seconde
Masque d’approximation du Laplacien
Calcul
On a :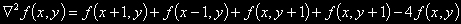
Masque associé
On définit les dérivées partielles du second ordre grâce aux filtres suivants :
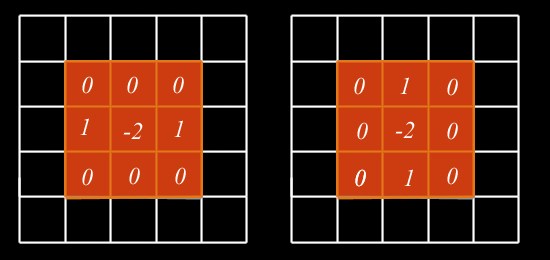
Ainsi, l'opérateur laplacien donne une approximation directe de la somme des dérivées secondes, ce qui peut être obtenu avec la matrice sommant les deux précédentes :
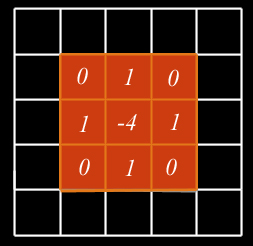
Variantes de ce filtre basées sur d'autres approximations :
Avantages et inconvénients
Bien que la méthode du laplacien respecte les contours formés, elle reste moins utilisée car plus sensible au bruit.
Pour éviter le bruit, on filtre l’image I avec un filtre G le plus souvent de type Gaussien :
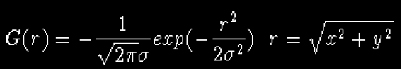
ayant pour Laplacien :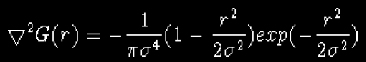 
plus connu sous le nom de "chapeau mexicain".
Le paramètre σ est destiné a régler la résolution à laquelle les contours sont détectés. On constate sur ces images l'évolution du niveau de détail en fonction de σ :
Marr et Hildreth
Cet opérateur est la combinaison d'un filtre Gaussien de paramètres de variance sigmaX et sigmaY avec un opérateur Laplacien (4-connecté).
Il s'agit d'un détecteur de contours permettant de limiter les amplifications des hautes fréquences des dérivées secondes par une gaussienne de variance ajustable.
Huertas et Medioni
Leur hypothese de travail est qu'au voisinage d'un passage par zero, l'image Laplacien peut être approximée avec un polynôme de degré 3 sur les lignes et les colonnes. Les passages par zero identiant les contours sont alors detectes de maniere analytique à l'aide de celui-ci et non plus sur l'image Laplacien.
Comparaison Gradient/Laplacien
Illustrations
Résultats
Les deux techniques sont assez proches. Globalement, le laplacien est plus sensible au bruit mais sa complexité est moindre surtout par rapport aux variantes directionnelles du gradient de type Sobel ou Prewitt. En effet, le laplacien nécessite une convolution, le gradient deux.
Au final, les points obtenus par ces deux techniques sont non-structurés, d'où la nécessité de post-traitements. Des filtrages ultérieurs simples comme le seuillage permettent de compenser le bruit mais leur enchainement est délicat.
Dérivation par filtrage optimal
Principe : les trois critères
Le résultat d'une détection de contours peut être évalué à l'oeil nu mais cela reste alors subjectif. Trois critères objectifs de performance d'un détecteur de contours ont été énoncés par Canny :
L’efficacité de détection
Il doit exister une faible probabilité de manquer un point de contour et de détecter un point qui n’en est pas un. L'efficacité de la détection se définit donc comme le quotient de la réponse du filtre à l'emplacement de la transition par la valeur efficace du bruit après filtrage.
On a : :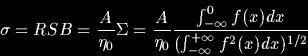
Le critère de localisation
Les points détectés comme contours doivent être aussi proches que possible des points de contours réels. Cela revient à maximiser l'écart type de la position des passages par zéro :
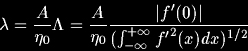
Le critère d'unicité
Un contour ne doit provoquer qu’une seule réponse de l'opérateur d'extraction, ce qui impose de minimiser l'expression :
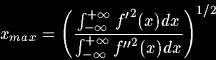
Opérateurs
Canny - Deriche
Calculs
L’obéissance à ces trois critères permet d’obtenir une équation différentielle dont la solution est :
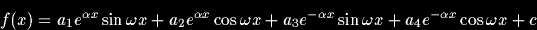Canny impose des conditions initiales à cette résolution d’équation mais ces dernières sont coûteuses en implémentation.
C’est pourquoi Dériche les a redéfinies en vue d’effectuer un traitement récursif et donc plus rapide : l'opération de convolution est effectuée en un nombre fixe d'opérations par point de l'image. Le détecteur optimal donne une image résultat dans laquelle les contours seront localisés au maximum du gradient de l'image initiale convolué avec une gaussienne de Deriche. Les conditions aux limites sont données par :
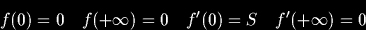
On obtient alors : a1 = a2 = a4 = c = 0.
D'où le filtre optimal :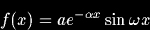 
Inconvénients
Le filtre de Dériche est anisotrope : il détecte mieux les coutours horizontaux et verticaux que les contours diagonaux.
De plus il ne faut l'utiliser que quand le rapport signal/bruit est inférieur à 1.
Shen – Castan
Shen et Castan ont adopté la même démarche que celle de Canny et Dériche mais leur formalisation des critères décrivant un détecteur de contour optimal est différente.
Calculs
Le filtre de lissage obtenu par Shen et Castan s'écrit :
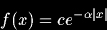avec 
et le filtre de dérivation correspondant :
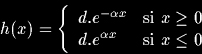avec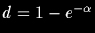 
Le paramètre α définit la largeur du filtre : plus il est petit, plus le lissage effectué par le filtre est important.
Avantages et Inconvénients
Le filtre de Shen et Castan est anisotrope et très sensible au bruit. Par contre, si l'écart-type de la gaussienne est élevé, l'opérateur sera robuste vis à vis du bruit, mais les contours seront mal localisés. Enfin, la discontinuité d'ordre 1 au point 0 du filtre peut entrainer la détection de contours multiples.
Identification des points de contour
Le calcul du gradient ou du laplacien, bien que constituant la partie essentielle de la détection des contours, ne fournit pas directement les points de contour.
A la fin de cette étape on obtient un classement des pixels de l’image en points contour et points non contour. Les points contours forment entre eux et selon leur emplacement des composantes connexes qui constituent des régions.
Point sur le seuillage
Le seuillage permet d'extraire le contour que l'on a détecté et de ne garder que les valeurs les plus significatives. On élimine ainsi les erreurs dues au bruit de l'image originale.
Approche gradient
Extraction des extréma locaux
On sélectionne les les passages par zéro de la dérivée de la norme du gradient dans la direction du gradient.
Pour cela, on détermine, pour un pixel p donné, les valeurs du gradient sur la droite passant par p et ayant pour direction celle de son gradient. On vérifie ensuite que le gradient en p est bien localement maximal sur cette droite.
Seuillage par hystérésis
On effectue ensuite un seuillage par hystérésis de l'image des maximums locaux (avec valeurs de la norme du gradient)
Le principe est d'utiliser deux seuils pour la norme du gradient : Sb (seuil bas) et Sh (seuil haut) et de sélectionner les pixels pour lesquels :
- la norme du gradient est supérieure à Sb;
- le pixel est connecté à un pixel pour lequel la norme du gradient est supérieure à Sh par un chemin constitué de pixels dont la norme du gradient est supérieure à Sb
Approche Laplacien
Extraction des des passages par zéro
Une fois le Laplacien calculé, on recherche ses passages par zéros et on crée une image de ces passages. Seuls les pixels pour lesquels le laplacien change de signe sont sélectionnés.
Seuillage
On élimine les points de trop faible gradient.
Pour cela, on effectue un seuillage des passages par zéro.
L’élimination des passages par zéro de faible norme peut s'effectuer par :
- algorithme de seuillage quelconque. (Ex : algorithme de seuillage par hystérésis précédemment décrit pour l'approche gradient.)
- méthodes basée sur le suivi de frontières et sur un calcul local du gradient. Ainsi, les passages par zéro extraits définissent des lignes fermées délimitant les régions de points connexes où le laplacien est positif ou négatif.
Paramétrage du seuillage
Les deux paramètres du seuillage par hystérésis jouent sur la détection des contours. Le seuil bas sert à éliminer le bruit et le seuil haut permet d'écarter les faux contours qui peuvent avoir été détectés.
Ainsi, plus le seuil bas sera faible et le seuil haut élevé, plus il y aura de contours détectés au détriment du bruitée. Il faut donc trouver un compromis.
Pré et post traitements
Pré-traitement
Les filtres larges de type Laplacien sont souvent précédés par des filtres passe-bas (filtres de lissage) à large support car ils sont très sensibles au bruit. Cela facilite le calcul de la dérivée. Pour cette opération, on choisit souvent un filtre gaussien. Or, ce filtre a le défaut de flouter l’image. La plupart du temps il faut donc combiner astucieusement filtre non linéaire et filtre linéaire. On peut aussi restaurer l’image afin d'en compenser les déformations.
Post-traitement
Les filtres passe-bas ou passe-haut peuvent aussi servir de finalisation à un filtrage pour réduire le bruit ou la quantité de détails par exemple.
On peut ensuite passer à l'étape de segmentation qui doit permettre de réaliser une partition de l'image en ensembles connexes homogènes (régions) afin de faciliter leur liaison et d'opérer à une « fermeture des contours ».
Le principe de ces méthodes consiste à prolonger les extrémités des chaînes ouvertes (composantes connexes) générées par l’extraction des points contour.
Pour cela, on va utiliser la direction estimée du contour au point extrémité afin de déterminer les points voisins candidats au prolongement du contour. Il s'agit de ceux perturbant le moins cette direction.